線形計画法の双対性を交代行列に関するシンプルな結果から出す方法
#数楽 メモhttps://projecteuclid.org/euclid.bams/1183522375 …John von Neumann's work in the theory of games and mathematical economicsH. W. Kuhn and A. W. Tucker1958
#数楽 以下、c,x∈R^m, b,y∈R^n, A∈M_{m,n}(R)とし、標準内積をb^T y=〈b,y〉と書く。x≧cはすべての成分で≧が成立していることを意味するものとする。続く
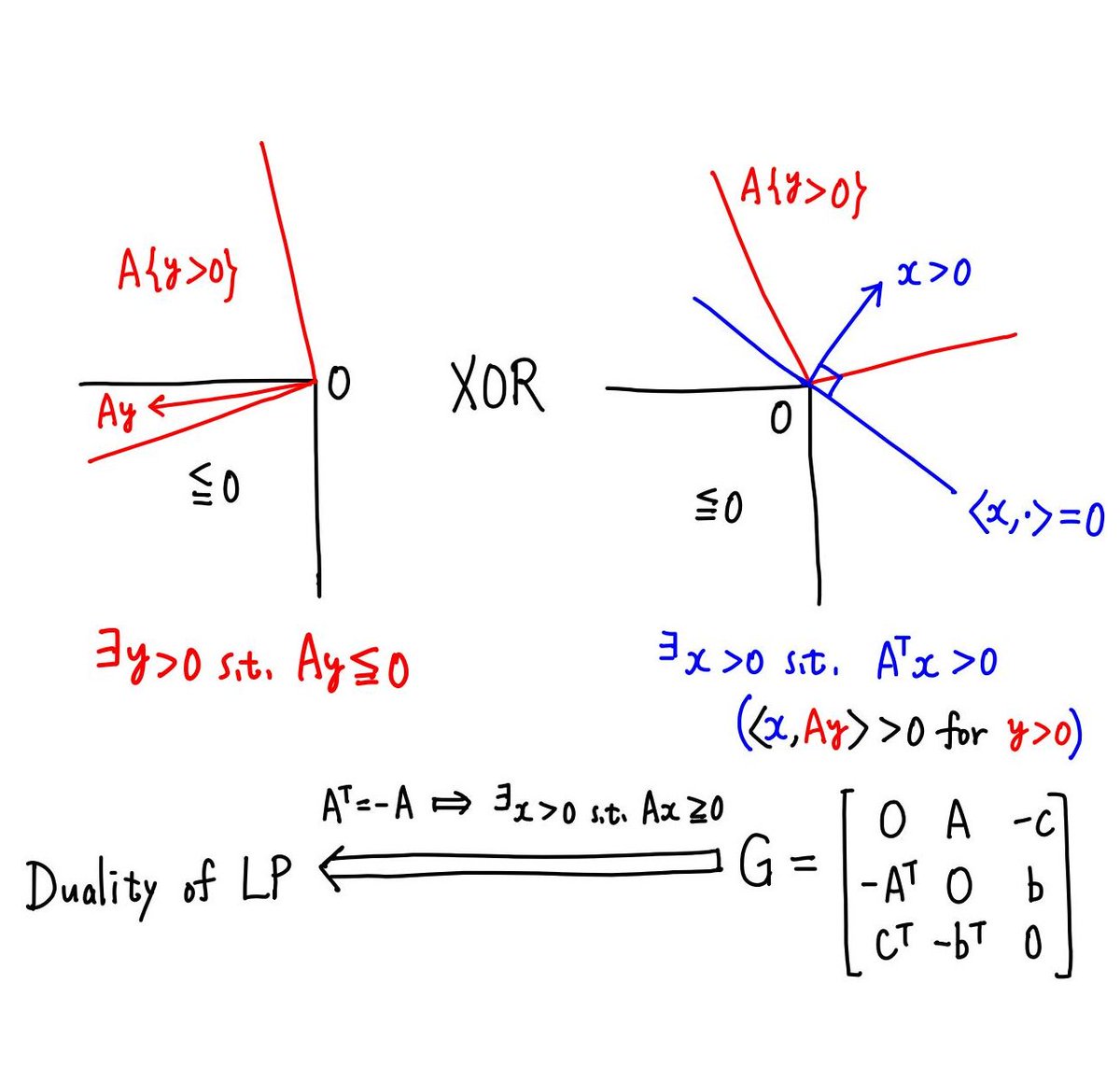
#数楽 定理:次のどちらかが成立している。・不等式 x>0, A^T x>0 の解が存在する。・不等式 y>0, -Ay≧0 の解が存在する。この定理は凸錐に関する直観があれば自明に感じられるはずの結果。後者の条件の否定は「すべてのy>0について、Ay≦0でない」。続く
#数楽 続き。開凸錐{Ay|y>0}が閉凸錐{x≦0}と共通点を持たないことを意味する。そのとき、ベクトルx>0で〈x,Ay〉>0 (y>0)を満たすものが取れること(後者の条件が成立すること)は図を描けば当然だと感じられるはずである。続く
#数楽 定理をAが交代行列(A^T=-A)の場合に適用すると、不等式x>0, Ax≧0の解が常に存在することがわかる。系:Aが交代行列ならば、不等式 x>0, Ax≧0 の解が存在する。
#数楽 続き。所謂、双対問題との関係は次のm+n+1次の交代行列Gを考えれば得られる。任意の実m×n行列Aに対してG=[ 0 A -c][-A^T 0 b][c^T -b^T 0]さらにw=[x][y][z]とおく。
#数楽 このとき、不等式の不等式w>0, Gw≧0の解が存在する。もしもz>0ならば解をzで割ってz=1とできる。その解は以下を満たしている。x≧0A^T x≦by≧0Ay≧c〈x,c〉≧〈b,y〉続く
#数楽 続き。最初の4つから、〈x,c〉≦〈x,Ay〉=〈A^T x,y〉≦〈b,y〉なので、その解はmax〈x',c〉=〈x,c〉=〈b,y〉= min〈b,y'〉を満たしている。ここで最小はx'≧0、A^T x'≦bについて取り、最大も同様。続く
#数楽 要するにz>0のケースは以下の双対問題達が解を持つ場合にちょうどなっているわけです。(P) x≧0、A^T x≦bのもとで内積〈x,c〉を最大化せよ。(D) y≧0、Ay≧cのもとで、内積〈b,y〉を最小化せよ。双対性は交代行列の作り方から出て来ています。
#数楽 以上の話題もまた完全に専門外なのですが、「双対性はより大きな世界を別の見方をすることによって出て来ることが多い」というパターンにはまっていて分かりやすいと思う。以上の議論では、m+n+1次の大きな交代行列から、線形計画法の双対性が分かりやすく出て来ている。
#数楽 「実交代行列Gに対して、非負の成分を持つ0でないベクトルwでGw≧0を満たすものが存在する」という超絶シンプルな結果を特殊な形の交代行列Gに適用するだけで線形計画法の双対性が出て来るわけです。
#数楽 ナマの主問題と双対問題を直接扱って線形計画法の双対性を解説している場合と、より大きな世界に埋め込むことによる以上の説明を比較すれば、後者の解説がどれだけシンプルであるかがよくわかると思います。
#数楽 https://twitter.com/genkuroki/status/841661525064589313 …リンク先で「開凸錐」という言い方をしてしまったが、その言い方は撤回する。全然開ではない。単に原点が除かれているだけ。
#数楽 例:A=1(スカラー)でbもcもスカラーであるとし、G=[ 0 1 -c][-1 0 b][ c -b 0]w=[x][y][z] x,y,z≧0と仮定する。Gw=[ y-cz ][-x+bz][cx-by]より~続く
#数楽 例続き。Gw≧0と次は同値:x≦bzy≧czcx≧byGw≧0かつz>0であるようなw≧0が存在することとx≦by≧ccx=byを満たすwが存在することは同値。たとえばb<0ならばw≧0(x,y,zは非負)からz=0となる。一般の場合も同様です。
#数楽 続き。次の文献に一般の行列Aを交代行列に埋め込んで線形計画法の双対性を出す議論が載っていました。ついさっき検索して発見した。http://dsl4.eee.u-ryukyu.ac.jp/DOCS/ipm/node3.html … (HTML版)http://dsl4.eee.u-ryukyu.ac.jp/DOCS/ipm.pdf (PDF版)
#数楽 このツイートが繋がっている線形計画法における双対性を出す話を論理的にフォローしたい人のための文献紹介。まず[1] A.W.Tucker, Dual systems of homogeneous linear systems (1950)続く
#数楽 続き。その論文(Tucker(1950))はhttps://books.google.co.jp/books?hl=ja&lr=lang_ja|lang_en&id=zfaUBDY33XkC&oi=fnd&pg=PA3&ots=aiBC8jrULr&sig=peEMWcudoAToYJg3RK4kQZZYVQs#v=onepage&q&f=false …https://books.google.co.jp/books?hl=ja&lr=lang_ja|lang_en&id=qdzTCwAAQBAJ&oi=fnd&pg=PP1&ots=siVKis9vsC&sig=osQyHnT8pD15WkevkBBVGfJA4mI#v=onepage&q&f=false …で読めます。その定理3が必要な結果。続く
#数楽 Tucker(1950)定理3:任意の実m×n行列Aに対して、あるx∈R^mとy∈R^nが存在して、x≧0, A^T x≧0y≧0, Ay≦0x-Ay>0, A^T x+y>0.ここで、≧,>はそれぞれすべての成分で≧,>が成立していることを意味する。続く
#数楽 続き。GがN次実交代行列のとき、G^Tに前定理を適用すると次が得られる("v=x+y")。系:N次実交代行列Gに対して、あるv∈R^Nが存在して、v≧0, Gv≧0, v+GV>0. ここで≧,>はそれぞれすべての成分で≧,>が成立することを意味する。続く
#数楽 続き。そして、G=[ 0 A -c][-A^T 0 b][ c^T -b^T 0]に上の系を適用すると(P) min{〈x,c〉|x≧0,A^T x≦b}(D) max{〈b,y〉|y≧0,Ay≧c}の双対性が得られます。
#数楽 続き。系から存在が保証されるv≧0, Gv≧0, v+Gv≧0を満たすv∈R^{m+n+1}をv=[x][y][z]と書いてちょっとした議論を行うことになります。そこから先はリンク先で紹介した文献と同じ。https://twitter.com/genkuroki/status/841981145289965568 …
#数楽 訂正。一つ前のツイートの「v+Gv≧0」は正しくは「v+Gv>0」(すべての成分が正)です。z>0の場合は簡単。問題はz=0の場合なのですが、その場合にv+Gv>0が保証されていることが大活躍します。
#数楽 z=0のときのv+Gv>0の最終行より、〈x,c〉>〈b,y〉が出ます。だから、〈x,c〉>0または〈b,y〉<0となるのですが、前者のとき、y≧0,Ay≧cとなることは不可能になり、x≧0,A^T x≧bなるxが存在すれば〈x,c〉は幾らでも大きくなります。後者も同様。
#数楽 ググると代数的に行けるところを解析的に処理していたりする解説がたくさん見つかりますが、1950年代的な方法の方がシンプルだったりします。H.Weylさんも「ミニマックス定理の初等的証明」という論文を書いていたりする。
#数楽 追加https://scholar.google.co.jp/scholar?cluster=16593289419580139542&hl=ja&as_sdt=0,5 …Broydenに定理:直交行列Pに対して、成分が全て正のベクトルvと対角成分が全て±1の対角行列Dが存在して、Pv=Dvとなる。これの初等的で複雑な証明を与えているのですが、概念的でシンプルな証明はあるのか?
#数楽 リンク先の質問(Farkasの補題から上で紹介した「系」を出す方法)については、このツイートが繋がっている返答連鎖で紹介した論文Tucker(1956)の最初の補題と定理1の関係を見ると納得しやすいと思う。http://math.stackexchange.com/questions/1203122/tuckers-theorem-from-farkas-lemma# …
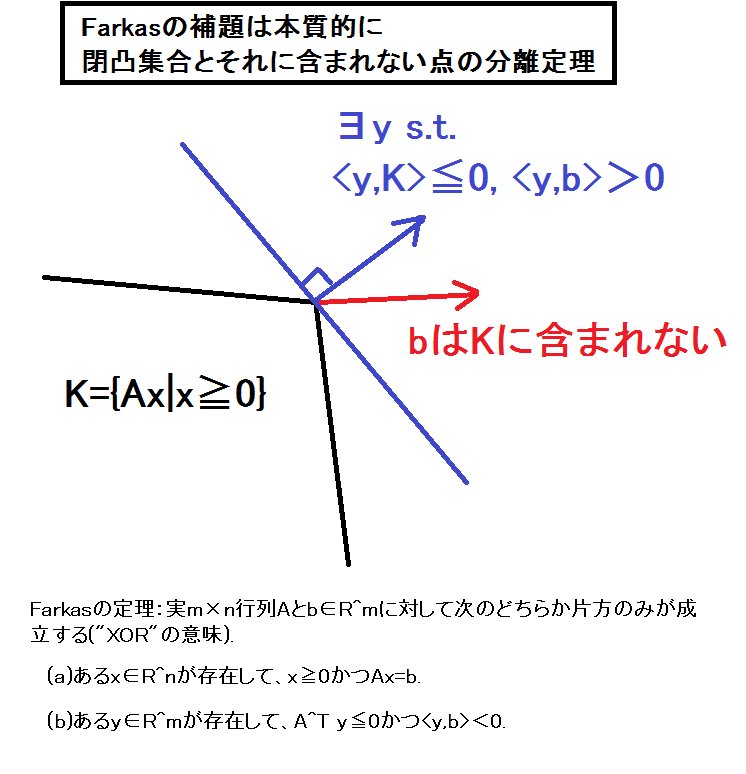
#数楽 Farkasの補題は本質的に閉凸集合とそれに含まれない点の分離定理(の易しいバージョン)です。だから証明の仕方がものすごくたくさんある。"Yet Another Proof of Farkas's Lemma" な世界になっていることがググると確認できる。pic.twitter.com/PuOh0mUJl1
#数楽 N次の実交代行列Lと単位行列EとR^Nの標準基底e_iに対するA=[L,-E]、b=e_iにFarkasの補題を適用すると補題:N次実交代行列Lと任意のi=1,…,Nについて、あるx_i∈R^Nが存在して、x_i≧0かつLx_i≧0かつx_i+Lx_iの第i成分は正。
#数楽 続き。この補題のx_iの総和をxとすると定理(Tucker(1956)):N次実交代行列Lに対してあるx∈R^Nが存在して、x≧0かつLx≧0かつx+Lx>0 (ベクトルx+Lxのすべての成分は正)。この定理の表現論的な証明ってあるんですかね?
#数楽 続き。訂正。Tucker(1956)ではなく(1950)。この定理をL=G=[ 0 A -c][ -A^T 0 b][ c^T -b^T 0]に適用すると線形計画法の強双対定理が得られることを、この返答連鎖ですでに説明した。
#数楽 続き。以上のような話はCayley変換で直交行列の話とも結び付き、次のような定理も得られているらしい。Broydenの定理:直交行列Qに対して、あるベクトルv>0と対角成分がすべて±1の対角行列Dが存在して、Qv=Dv.これもある種の不動点定理。
#数楽 続き。ゲームの対称化は元祖フォン・ノイマンさん自身も考えていました。例えば将棋は先手と後手で非対称なゲームなのですが、盤駒を二組用意して、互いに先手と後手の両方を受け持って将棋を指せば対称ゲームになります。行列の場合でも同様の操作が可能。
#数楽 続き。行列で書ける対称ゼロ和ゲームの典型例はじゃんけん。じゃんけんでグー・チョキ・バーのそれぞれで勝ったらa,b,cのお金を相手から巻き上げるギャンブルは[ 0 a -c ][ -a 0 b ][ c -b 0 ]の形の交代行列が対応しています。
#数楽 実交代行列に関するTuckerの定理を使ってBroydenの定理「任意の回転の仕方Qに対して全ての成分が正のベクトルでQによる回転の後に全ての成分をその絶対値で置き換える操作で不変なものが存在する」を示しましょう。文献は→ https://pdfs.semanticscholar.org/ba0e/2f6f7574643f1ae6d9306ce264cdd2dabfb5.pdf …
#数楽 n次元ユークリッド空間の原点を固定した回転は行列式が1のn次直交行列Qで表現できます。Qが直交行列であるとは、Qは実正方行列で、その転置Q^TがQの逆行列Q^{-1}になることです。回転(と鏡映変換)が直交行列で表現できることを知るだけで線形代数を学ぶ価値がある。
#数楽 Aが交代行列であるとは、Aが実正方行列であり、A^T=-Aが成立することです。Aが交代行列ならば、そのexponential exp(A)は行列式が1の直交行列(回転を表現する行列)になります。ここまで理解できれば線形代数を勉強した価値が出て来ます。
#数楽 行列は様々なものを表現するための極めて柔軟で便利な道具になっています。行列で書ければコンピュータにものることが多く、極めて実用的な道具でもあります。行列の道具箱に入っている各種道具達をマスターするには結構時間がかかるのですが、そうする価値があります。
#数楽 工作好きの子供が様々な工具が入った道具箱を買ってもらったときの喜びと同じような嬉しさを感じながら勉強できれば、数学の勉強は常に楽しいままになるはずです。私にとって数学的な事柄はすべて「学校のお勉強」でも受験対策でもなく、「楽しい工作」と同じようなことでした。
#数楽 Aが交代行列のとき、exp(A)が直交行列になるだけではなく、Q=(E-A)/(E+A)も直交行列になります。行列なのに分数表記を使っていますが、算数で習う分数表記は分子と分母が可換ならそのまま有効になります。大学レベルの話と算数は当然結びついています。続く
#数楽 行列の転置と逆行列を取る操作は可換なので、Q=(E-A)/(E+A)のとき、A^T=-Aならば、Q^T=(E+A)/(E-A)=Q^{-1}となり、Qは直交行列になります。これをCayley変換と呼ぶようです。続く
#数楽 Q=(E-A)/(E+A)をAについて逆に解くと、A=(E-Q)/(E+Q)となりますが、Q^T=1/Qならば、A^T=(E-1/Q)/(E+1/Q)=(Q-E)/(Q+E)=-Aとなり、Aは交代行列になります。
#数楽 高校数学と繋げるための演習問題:次の行列Qが直交行列であることを確認し、Q=(E-A)/(E+A)をみたす交代行列A=(E-Q)/(E+Q)を求めよ。Q=[cos θ -sin θ][sin θ cos θ]この直交行列は平面の回転を表現しています。
#数楽 2×2の直交行列の話は本質的に高校で習う三角函数論そのものだと思って構いません。三角函数を使えば平面の回転を数学的に表現でき、2×2の直交行列でも表現でき、それらは本質的に同じ話になっているわけです。これを理解するだけでも線形代数を学ぶ価値がある。
#数楽 平面の回転は一般のn次元空間の回転の話に一般化されます。それが直交行列による直交変換の理論。三角函数の理論のn次元の場合への一般化でもあります。3次元の場合は3Dグラフィクスを扱うプログラミングで必須の道具。高速フーリエ変換も直交変換の一種。理系的には知らないと困る話。
#数楽 実交代行列に関するTuckerの定理:AがN次実交代行列のとき、あるv∈R^Nが存在して、v≧0かつAv≧0かつv+Av>0となる。ここで≧,>はすべての成分で≧,>が成立することを意味するとする。証明はすでに解説してある。v+Av>0とできることが最重要ポイント。
#数楽 このTuckerの定理よりも、Farkasの定理の方がよく使われているようですが、Farkasの定理は任意の行列に適用できる点で便利なのですが、Tuckerの定理を適用するときに作られる交代行列が意味ありげになる点は捨て難いと思います。(交代行列は対称ゲームと解釈可能)

#数楽 続き。直交行列Qに対してサイズが3倍の交代行列Aを添付画像のように定めてTuckerの定理を適用すると、Broydenの定理がただちに得られます。トポロジカルな議論でも証明できそうですね。トポロジカルな証明を見付けた人がいたら #数楽 タグで紹介して下さい。pic.twitter.com/YitAe9RW8h
#数楽 2×2の回転行列Qに対するA=(E-Q)/(E+Q)の計算は複素数でやった方が楽な人が多いと思う。q=e^{it}のとき分子分母をe^{it/2}で割って整理すると、a=(1-q)/(1+q)=-i tan(t/2). 続くhttps://twitter.com/genkuroki/status/842900777978929152 …
#数楽 続き。Aは-i tan(t/2)に対応する2×2行列で、A=(E-Q)(E+Q)^{-1}=[ 0 tan(θ/2)][-tan(θ/2) 0 ].1は2×2の単位行列に対応し、虚数単位iは[ 0 1][-1 0]に対応。
#数楽 Cayley変換の応用:q=e^{iθ}のときa=(1-q)/(1+q)=-i tan(θ/2)、q=(1-a)/(1+a)から、よく使われる有理化の公式「t=tan(θ/2)とおくとcos θ=(1-t^2)/(1+t^2)、sin θ=2t/(1+t^2)」が出ます。

#数楽 ちなみにtan(θ/2)の正体は「xy平面上の原点を中心とする単位円周の点(cos θ, sin θ)における接線と直線x=1の交点のy座標」です。図を描くと合同な直角三角形が見えるのでθ/2が出て来る理由がわかる。pic.twitter.com/ZlUXKm7SCj
#数楽 訂正:以上の話の流儀では、虚数単位iに対応しているのは、[ 0 1][-1 0]ではなく、I=[0 -1][1 0]の方。このIについてexp(θI)=(cos θ)E+(sin θ)Ihttps://twitter.com/genkuroki/status/843073702946197505 …
#数楽 続き。「Broyden⇒Tucker」の証明は交代行列Aから直交行列QへのCayley変換Q=(E-A)/(E+A)を使えば瞬殺。逆もA=(E-Q)/(E+Q)を使えれば同様なので、Qが固有値-1を持たなければ瞬殺なのですが、その制限を外すためには工夫が必要だろう。続く
#数楽 続き。一つ前のツイートで「リンク先」という言い方で言及したのは次のリンク先です。https://twitter.com/genkuroki/status/842925793118380033 …
#数楽 以上の話題は大学1年レベルの線形代数の話。証明はフォローできたら終わりじゃなくて、その周辺をうろうろ自力で歩き回ってみて、どこが賢いのかについて感覚をつかむことが大事。上の話では、つまらない交代行列や直交行列の具体例でつまらない具体的な計算を色々してみることも大事。

#数楽 Farkasの補題、実交代行列に関するTuckerの定理、線形計画法における強双対性、直交行列に関するBroydenの定理に関するまとめを放流開始線形計画法の強双対性を出すまでの部分のまとめpic.twitter.com/ZU03ECS2vr





#数楽 線形計画法の双対性が、交代行列による双対性の表現とCayley変換を通して、直交変換Qと成分ごとに絶対値を取る操作の合成に関する不動点定理 "|Qx|=x>0" (Broyden)と繋がっているというような話をつい最近まで知りませんでした。
#数楽 この周辺の話題(ミニマックスやら線形計画法の双対性やら)では、「Brouwerの不動点定理」だけではなく、「Browderの不動点定理」が出て来てややこしいのですが、ついに「Broydenの不動点定理」まで出て来て、見間違え易い状況が発生してしまっている!(笑)
#数楽 交代行列に関するTuckerの定理:実交代行列Aに対して、あるベクトルvでv≧0、Av≧0、v+Av>0を満たすものが存在する。Tuckerの定理から等号の束縛条件を含む場合の結果を出す例として「Tuckerの定理⇒Farkasの定理」の証明を紹介。続く
#数楽 Farkasの定理(以下補題):任意の実m×n行列Mとb∈R^mに対して、次のどちらか片方のみが成立する。(1)あるx∈R^nが存在してx≧0、Mx=b.(2)あるy∈R^mが存在して-M^T y≧0、b^T y>0.条件(1)の束縛条件が等式が入っている。続く。
#数楽 「Tuckerの定理⇒Farkasの定理」の証明。もしも(1)と(2)が同時に成立しているとしたら、0<b^T y=x^T M^T y≦0となって矛盾する。だから(1)または(2)が成立することを示せばよい。交代行列を次のように定める。続く
#数楽 続きA=[ 0 -M^T M^T 0][ M 0 0 -b][-M 0 0 b][ 0 b^T -b^T 0].Tuckerの定理より、あるv=[x][y'][y''][z]が存在して、続く
#数楽 続き、v≧0、Av≧0、v+Av>0となる。z>0のとき、vをzで割ってz=1とすると、Av≧0からMx≧b、-Mx≧-b、つまりMx=bとなる。z=0のときy=y'-y''とおくと、Av≧0より-M^t y≧0となり、v+Av>0よりb^T y>0となる。q.e.d.
#数楽 続き。要するに「X=0 ⇔ X≧0 かつ X≦0」なので「≧0」で「=0」を表現できるだけの話です。このツイートが繋がる返答連鎖を全部フォローすれば線形代数がどのように役に立つかの一例(線形計画法の強双対性の証明)を知ることができます。
#数楽 続き。「任意の実行列に関するFarkasの補題」「実交代行列(対称ゼロ和ゲーム)に関するTuckerの定理」「直交変換してから各成分の絶対値を取る操作に関するBroydenの不動点定理」はどれも数学的に同じ深さにあり、どれか一つを仮定すると他は容易に証明されます。



